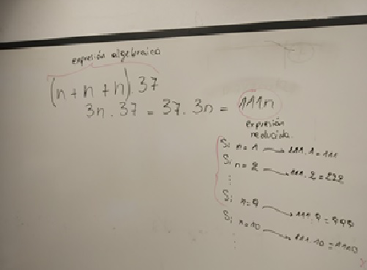El Plan CEIBAL y el uso de tecnología digital con sentido pedagógico para la enseñanza de la Matemática. El caso de la Placa micro:bit

Gustavo Bentancor Biagas (1) 

Lily Velázquez (1) 

Ana Laura Machado (1) 

Ignacio López (1) 

(1) Plan CEIBAL, Uruguay

Resumen. El artículo que presentamos se basa en una investigación cuyo objetivo fue identificar y describir el uso que realizan de la placa micro:bit con sentido pedagógico los profesores de Matemática de 1ero. y 2do año. de Educación Media de Uruguay. Se realizó un estudio a través de un modelo indagativo cimentado en el paradigma cualitativo. Las técnicas que se desarrollaron fueron: grupo de discusión con 8 profesores y análisis documental de las propuestas de 14 docentes. Entre los principales hallazgos del estudio, se destaca que el uso que hicieron los profesores de la placa micro:bit permitió mejorar la comprensión de conceptos matemáticos (divisibilidad, relaciones de orden, variable) y posibilitó que los alumnos abordaran la situación con una actitud reflexiva que los predispuso a formular conjeturas y discutir su validez. Asimismo, la Programación en la clase de Matemática permitió a los profesores organizar las actividades pedagógicas de una manera innovadora que no se hubiese logrado sin la placa. Los docentes concuerdan que, en las interacciones entre los participantes y en la construcción conjunta de docente y alumnos de conceptos matemáticos y habilidades digitales con la finalidad de resolver la situación, se pudo constatar el potencial transformador de la tecnología digital.

Palabras clave: Plan CEIBAL; enseñanza de la Matemática; profesores de Matemática de educación media; tecnología digital; placa micro:bit

O Plano CEIBAL e o uso da tecnologia digital com sentido pedagógico para o ensino da Matemática. O caso da Placa Micro:bit

Resumo. Este artigo baseia-se numa pesquisa cujo objetivo era identificar e descrever o uso da placa Micro: bit para ensinar professores de Matemática do 1º e 2º ano do Ensino Médio no Uruguai. O estudo realizou-se através de um modelo de pesquisa qualitativa. As técnicas utilizadas foram: grupo de discussão com 8 professores e análise documental das propostas de 14 professores. Entre as principais conclusões do estudo, destaca-se que o uso feito pelos professores da placa Micro: bit melhorou a compreensão dos conceitos matemáticos (divisibilidade, relações de ordem, variável) e permitiu aos alunos abordarem a situação com uma atitude reflexiva, induzindo-lhes a formular conjecturas e a discutir a sua validade. Por outro lado, a Programação na aula de Matemática possibilitou aos professores organizar atividades pedagógicas de uma forma inovadora que não teria sido possível sem a placa. Os docentes concordam que, nas interações entre os participantes e na construção conjunta de conceitos matemáticos e habilidades digitais por parte do professor e dos alunos para resolver a situação, pôde-se notar o potencial transformador desta tecnologia digital.

Palavras-chave: Plano CEIBAL; ensino de Matemática; professores de Matemática de educação média; tecnologia digital; Placa Micro:bit.

Plan Ceibal and the use of digital technology with pedagogical sense in math teaching. The case of the micro:bit board

Abstract. This article is based on research aiming to identify and describe how Uruguayan 7th and 8th grade mathematics teachers use the micro:bit microcomputers with pedagogical sense. The study used an indagative method based on a qualitative paradigm. The developed techniques were: discussion groups with eight teachers and document analysis of materials presented by fourteen teachers. Among the main discoveries of this research, it stands that the use teachers made of the micro:bit board allowed a better understanding of the mathematical concepts by their students (divisibility, order relations, variables) and it allowed them to approach the situation with a reflective attitude that predisposed them to build conjectures and discuss their viability. On the other hand, programming in the maths class allowed teachers to organize the pedagogical activities in an innovative way that wouldn’t be possible without the board. Teachers agree that, in the interactions of the different participants, and the conjoint construction of mathematical concepts and digital skills between students and them aiming to solve a specific situation, the transformative potential of digital technology became evident.

Keywords: Plan CEIBAL; mathematics teaching; middle school math teachers; digital technology; micro:bit board

1.  Introducción

El Plan de Conectividad Educativa de Informática Básica para el Aprendizaje en Línea (Plan CEIBAL) se creó en 2007 siendo parte de políticas educativas para el desarrollo de la inclusión e igualdad de oportunidades de todos los niños y jóvenes, con el objetivo de apoyar con tecnología las prácticas de enseñanza y aprendizaje en las aulas uruguayas. Se constituye como una sostenida inversión de Uruguay en tecnologías digitales para las instituciones, basado inicialmente en el proyecto OLPC (One Laptop Per Child), en que se distribuye un equipo por niño y se otorga conectividad a las instituciones educativas.

Uruguay ha logrado avances significativos en relación con el acceso de dispositivos y de disponibilidad en la conectividad, democratizando el acceso a la información y disminuyendo la brecha digital existente entre los diferentes sectores de la población. CEIBAL ha llevado adelante acciones para promover prácticas de enseñanza y aprendizajes significativas en territorio, haciendo foco en las construcciones de los actores protagonistas y sus necesidades. Especialmente la Gerencia de Formación ha logrado desplegar propuestas de intervención para la formación continua de los docentes y sus procesos de profesionalización. Dentro de esta gerencia el Departamento de Matemática ha generado diversas acciones tendientes a potenciar, buenas prácticas para la enseñanza de la matemática en los colectivos docentes tanto de la educación primaria como en la educación media.

Las diferentes experiencias y estudios asociados tanto a nivel regional como internacional dan cuenta de una insuficiencia en la dotación de equipamiento y conectividad para evidenciar mejoras en los aprendizajes asociados a dicha incorporación. La necesidad de un cambio metodológico radica en los diferentes usos que el docente reconoce en la tecnología, entendiendo que la sola presencia de ellas en las aulas no es un generador de cambios en cuanto a la apropiación y desarrollo de aprendizajes (Rivera-Vargas y Cobo-Romani, 2020).

A pesar de los avances realizados en cuanto al acceso a información, a los dispositivos y a la conectividad, hay desafíos que permanecen latentes y muy vigentes, fundamentalmente en lo que tiene que ver con la incorporación de herramientas digitales con sentido pedagógico.

2.  La evidencia internacional y nacional

Diversas investigaciones (Revelo, 2017; Goehle y Wagaman, 2016; Attard, 2015) señalan las ventajas de utilizar tecnología digital para la enseñanza de la Matemática, ya que proporcionan un escenario de visualización, exploración, manipulación e interacción entre el pensamiento intuitivo de los alumnos y los objetos matemáticos abstractos.

Sin embargo, la simple incorporación de la tecnología digital en las aulas de Matemática no garantiza la transformación de las prácticas educativas que conlleven a la mejora de los procesos de enseñanza y aprendizaje (Revelo, 2017; Attard, 2015; Bansilal, 2015). Algunos autores (Revelo, 2017; Goehle y Wagaman, 2016; Sosa, 2015) señalan que existen una serie de factores, como: la formación docente en habilidades y competencias digitales, el uso de aplicaciones digitales para la didáctica de la enseñanza de la Matemática y la promoción de redes de comunicación entre docentes y estudiantes para el aprendizaje colaborativo en torno a la tecnología, que tienen incidencia en la transformación de las prácticas.

En el caso de Uruguay, un estudio reciente (Vaillant, Rodríguez-Zidán, Bentancor-Biagas, 2020) ha evidenciado que el escenario es similar a la realidad internacional relatada en esto aspectos, pues si bien la disponibilidad de recursos tecnológicos en los centros educativos es muy favorable, existe un uso moderado de las tecnologías digitales con un sentido pedagógico, subutilizando algunos recursos como GeoGebra, Plataforma Adaptativa de Matemática (PAM), Plataforma CREA, entre otros. Si bien existen cada vez más aplicaciones y softwares que tienen el potencial para generar escenarios para la mejora de la comprensión de los conceptos matemáticos y de las habilidades digitales para innovar, indagar y crear nuevos procesos de enseñanza y aprendizaje, los resultados señalan que el mero uso de la tecnología digital no produce una mejora en las prácticas de enseñanza.

3.  Formulación del problema de investigación

Tal como lo señala la literatura internacional y la realidad de Uruguay, es importante conocer cómo la tecnología digital puede ser utilizada por los docentes con el fin de diseñar experiencias de enseñanza de la Matemática que permitan transformar sus prácticas y contribuya a enriquecer y fortalecer las propuestas de aula, para que los estudiantes puedan conseguir aprendizajes significativos de los conceptos matemáticos (García-González, y Solano-Suárez, 2020). En casi todos los contextos educativos se reconoce una tendencia de los docentes a la incorporación en sus prácticas de las tecnologías educativas, principalmente recursos web y dispositivos como computadoras, celulares inteligentes o tablets, sin embargo, no está tan claro el uso pedagógico de esta incorporación ni la transformación de sus prácticas reflexionadas desde ella. La experiencia relevada y la literatura específica a nivel internacional da cuenta que los esfuerzos realizados a niveles de políticas educativas, que intentaron dotar de equipos, conectividad, softwares específicos a los diferentes sistemas educativos a través de sus docentes y estudiantes, no son suficientes ni muestran una relación significativa con la mejora de los aprendizajes (Kozma, 2005; Valiente, 2010).

El estudio que se presenta en este artículo parte de una experiencia desarrollada en Uruguay durante el año 2020, en un nuevo escenario educativo producto de la situación de pandemia causada por el COVID-19, con alumnos de 1er. y 2do año de Enseñanza Media Básica, es decir con edades entre 12 y 15 años. Esta propuesta, llamada Encuentro Matemático, es una actividad anual de acompañamiento y de trabajo con estudiantes y docentes. En la misma, el equipo de Matemática de CEIBAL genera y plantea una serie de actividades, retos y desafíos para que cada docente trabaje junto a sus estudiantes, en su clase, integrando las tecnologías al aprendizaje de la matemática.

Las actividades se desarrollan en un entorno gamificado, buscando la generación de exploración, construcción y trabajo colaborativo. Uno de los retos propuestos para el 2020 involucró el uso de micro:bit, pequeña placa programable diseñada para que los estudiantes con escaso o ningún conocimiento de la programación puedan ejecutar un programa. Estas placas pueden recibir un conjunto de datos que el programa utilizará para producir una acción en concreto. Los datos (entrada) son suministrados al programa por los alumnos mediante sensores y las acciones (salida) a través de actuadores. Los sensores que comúnmente se utilizan son: brújula, acelerómetro sensor de luz ambiente (pantalla), botones, termómetro y los actuadores: pantalla (LED).

El estudio toma en cuenta las consideraciones antes señaladas y a partir de ellas se formulan las siguientes preguntas:

¿Qué importancia le dan los docentes de matemática de Educación Media al uso de la tecnología digital en sus prácticas de enseñanza?

¿El uso que hacen los docentes de matemática de la placa micro:bit podría incidir favorablemente en la mejora de la enseñanza de la matemática?

¿El uso de la placa micro:bit promueve el desarrollo de habilidades digitales y competencias generales o específicas a la matemática en los estudiantes?

¿Cómo integran los docentes la tecnología digital a sus procesos de enseñanza?

El estudio buscó contribuir a generar mayor conocimiento que se fundamente en la investigación empírica y que permita saber cómo los profesores de matemática de Educación Media de Uruguay utilizan la tecnología digital con sentido pedagógico para mejorar la comprensión de los conceptos matemáticos.

En esta línea, la investigación que se detalla tiene como objetivo identificar y describir el uso de la placa micro:bit con sentido pedagógico que realizan en sus clases los profesores de Matemática de 1ero y 2do año del Educación Media de Uruguay.

4.  Marco teórico de referencia

Se utilizó el modelo SAMR, Puentedura (2006), para colaborar con los docentes a incorporar las tecnologías digitales en la enseñanza, con el fin de lograr altos niveles de aprendizaje. Es un acrónimo que en inglés implica las acciones de sustitución, aumento, modificación y redefinición. A su vez estas cuatro acciones están diferenciadas en dos niveles: un primer nivel que muestra una mejora y un segundo nivel que reconoce una transformación. Específicamente, el primer nivel en la incorporación de la tecnología está dado por la Sustitución, y se evidencia en un aula en donde la tecnología sustituye directamente una herramienta sin ningún cambio funcional. En este nivel, la tecnología además de no ser decisiva en la construcción del conocimiento tampoco es imprescindible, ya que la tarea se hubiera podido realizar sin ella. En el siguiente escalón, y aún dentro de la categoría mejora, se produce el Aumento. En este caso además de que se realiza una sustitución de una herramienta por otra, se da una mejora en la funcionalidad de esta. En este nivel si bien la tecnología genera un valor agregado a la tarea, no se reconocen cambios metodológicos. El avance al siguiente nivel permite dejar lo que es considerado explícitamente como mejora, para pasar a ser un proceso de transformación en la Modificación. Se produce un avance en la función de la tecnología en donde aquí, ésta permite un rediseño significativo de las actividades de enseñanza. El último nivel de los cuatro, y segundo dentro de la categoría Transformación, se encuentra la tecnología permitiendo redefiniciones, creaciones de nuevas actividades en donde sin ella sería imposible llevarlas a cabo. Aquí claramente se produce un cambio metodológico.

Según plantea Vaillant (2015) en el prólogo del libro “Educación y Tecnología en el Uruguay: una mirada desde la investigación” existen tres categorías de elementos para tener en cuenta a fin de asegurar una adecuada incorporación de tecnologías digitales por parte de los docentes, en procesos con intención de enseñanza. Dichas categorías son las concernientes a la competencia tecnológica docente, la actitud frente a ella y el tipo de uso que le da. De esta manera aparece que el estar familiarizado con las tecnologías y disponer de dispositivos y conectividad, no alcanzaría para que la incorporación sea exitosa y genere aprendizaje, ya que aparecen en escena temas como la actitud del docente frente a la transformación que esta incorporación supone y la posibilidad de un cambio en las metodologías a tales efectos. El docente tiene que conocer las tecnologías digitales, creer en ellas como herramienta de cambio y estar dispuesto al cambio metodológico para la transformación de las prácticas áulicas.

En el mismo sentido, Tedesco (2012) distingue dos aspectos en lo que tiene que ver con el proceso de incorporación de las tecnologías digitales en los ámbitos educativos, asociado al carácter social, de acceso a la comunicación e información; y otra de carácter pedagógico, y en este último caso esa inclusión será vista como una herramienta pedagógica y didáctica para la transformación de las prácticas de enseñanza y con impacto en los aprendizajes. Especialmente y coincidiendo con la mirada actual de la literatura especializada a nivel internacional, Tedesco (2012) plantea la necesidad de sacar el foco en las tecnologías mismas y ponerlo en los modelos metodológicos que faciliten su incorporación y uso para su uso pedagógico.

Asimismo, Dussel (2011) se suma al cambio institucional en cuanto a las formas de incorporación de las tecnologías digitales en ámbitos educativos, planteando la necesidad de modificar la forma de configurar la creación de conocimiento en la escuela.

Las nuevas tecnologías tienen lógicas y modos de configurar el conocimiento muy diferente a los de la escuela. Las primeras funcionan en base a la personalización, la seducción y el involucramiento personal y emocional, y suelen ser muy veloces y con una interacción inmediata. La escuela, en cambio, es una institución basada en el conocimiento disciplinar, más estructurada, menos exploratoria, y con tiempos y espacios determinados de antemano, más lentos y menos porosos (Dussel, 2011, p. 11).

En tanto la intencionalidad pedagógica asociada a este uso de las tecnologías digitales en el ámbito educativo puede definirse según Coll (2004), el uso pedagógico de las TIC como una herramienta vital que mejora los procesos de enseñanza y de aprendizaje permitiendo orientar y brindar a los docentes la posibilidad de innovar sus prácticas de aula, creando entornos de aprendizaje más dinámicos e interactivos para la adquisición de un aprendizaje significativo estimulando los procesos mentales, facilitando el trabajo en equipo y las relaciones interpersonales. Lo que hace la diferencia en esta conceptualización del uso de las tecnologías digitales es el objetivo de que a partir de ella se promueva un aprendizaje significativo, poniendo foco en ese uso sin desconocer el elementos motivador y dinámico. Esto último igualmente puede ser abordado por múltiples herramientas, que serán digitales o no, pero en las cuales no necesariamente éstas desarrollan aprendizajes estables y duraderos.

Este uso pedagógico para Coll (2004) así planteado tiene como objetivo reforzar, consolidar, resignificar y apoyar, llevando a la práctica situaciones, modelos o metodologías de abordaje pedagógico ya existentes o emergentes que pueden transformar los ambientes escolares para el aprendizaje; asimismo el autor afirma que “El uso pedagógico de un recurso tecnológico sólo puede identificarse y describirse en sentido estricto en el marco de una práctica o actividad en cuya realización interviene ese recurso” (pp.17-19).

En cuanto al concepto de objeto matemático, en el contexto de este artículo se retoma lo propuesto por Pecharromán (2014)

“Un objeto matemático es, o representa, una cualidad o una acción que tiene la función de organizar o interpretar un contexto. Así pues, los objetos matemáticos son una función organizativa o interpretativa del contexto. El objeto matemático tiene un origen e identidad funcional” (p.112).

Asimismo, se retoma de esta autora la importancia de las diferentes representaciones asignadas a los objetos matemáticos, que le otorgan dicha identidad y funcionalidad. En esa misma línea, las representaciones adquieren relevante porque permiten caracterizar al objeto matemático, así como contribuir a su interpretación. Al decir de Pecharromán (2014)

“Las representaciones del objeto matemático, como signos que permiten su expresión, contribuyen al desarrollo de su significado y permiten (los iconos) la interpretación de sus propiedades y relaciones internas, que también son caracterizadoras del objeto” (p.114)

5.  Métodos y materiales

Para responder a nuestras preguntas de investigación y contribuir al conocimiento en torno al uso de tecnología digital en la enseñanza de la Matemática con sentido pedagógico, se diseñó un estudio a través de un modelo indagativo cimentado en el paradigma cualitativo.

Dada la profundidad de la información que necesitábamos para responder a las preguntas formuladas, debimos recurrir a dos técnicas para la recolección de datos: grupo de discusión y análisis documental.

6.  Población y muestra

El universo que constituye este estudio está determinado por la condición de ser profesor de Matemática de 1ero o 2do año de Educación Media en Uruguay. El marco que se utilizó para la determinación de la muestra cualitativa de este estudio se constituyó a partir de los registros y bases de datos de los docentes que participaron durante la edición 2020 del concurso “Encuentro Matemático” organizado por el Departamento de Matemática del Centro CEIBAL.

6.1Grupo de discusión

Para conformar la muestra del grupo se tuvo en cuenta que lo importante de esta técnica es la comunicación entre los participantes, en especial poder captar la profundidad de la realidad estudiada, por lo que para la selección de la muestra se buscó seguir con los principios de la heterogeneidad estructural para muestras cualitativas (Valles, 1997). Para esto, se conformaron tres niveles estructurales: eje socioeconómico, eje espacial y eje temporal que quedaron definidos a partir de una serie de variables estructurales que recogen las características del colectivo de los ocho profesores que participaron del grupo. La Tabla 1 muestra los niveles y variables estructurales que permitieron definir la muestra.

Tabla 1. Niveles y variables utilizadas para estructurar la muestra

Niveles estructurales
Socio estructural	Espacial	Temporal
Género, Edad, Formación inicial, Posgrado, Experiencia en el cargo.	Departamento de Uruguay.	Durante el Ciclo 2020 en el que se desarrolló el concurso.

Fuente: elaboración propia.

6.2Análisis documental

La selección de las unidades de análisis para la conformación de la muestra se realizó siguiendo los mismos principios de heterogeneidad estructural planteados (Valles, 1997) propuestos para el grupo de discusión. La muestra quedó conformada por 14 profesores a los que se les solicitó autorización para utilizar los documentos que dan cuenta de su producción con relación a las diferentes estrategias elaboradas para la resolución del Reto 3 a través del uso de la placa micro:bit. La evidencia fue recogida a través de la plataforma de gestión de aprendizaje CREA1

Del total de profesores participantes del concurso, en la Categoría Mangangá, (43 profesores) se accedió a los documentos didácticos de 14 de ellos quienes conformaron la muestra. La tabla 2 muestra un resumen de los materiales que se utilizaron para la revisión documental.

Tabla 2. Resumen de la muestra de materiales recogidos

Tipo de documento	Proporcionado por el docente
Programación de la placa micro:bit	D1-D2-D3-D4-D5-D6-D7-D8-D9-D10-D11-D12-D13-D14
Fotográfico	D1-D2-D4-D5-D8-D10-D12-D14
Recurso audiovisual - Video	D1-D2-D3-D4-D5-D6-D7-D8-D9-D10-D11-D12-D13-D14
Comentarios de la resolución de la situación problemática planteada	D1-D2-D3-D4-D5

Fuente: elaboración propia.

7.  Instrumentos

7.1 Grupo de discusión

La elección del grupo de discusión como técnica para la recogida de información se basó en la riqueza que ésta proporciona y la posibilidad de ampliar la comprensión del objeto de estudio. Con esta técnica se buscó profundizar algunos de los temas que se evidenciaron con el análisis documental realizado a través de los vídeos y de las estrategias de resolución de la consigna de trabajo propuesta (Reto 3).

Este dispositivo metodológico posibilitó generar un microespacio para conocer las opiniones y recoger la información de un colectivo de docentes a partir de sus interacciones, y de sus opiniones que se derivan de las experiencias personales vividas durante la actividad. La relevancia de esta técnica no directiva es expuesta por Morgan cuando al respecto señala, “son útiles cuando se trata de investigar qué piensan los participantes, pero son excelentes para descubrir por qué los participantes piensan como lo hacen” (Morgan, 1988, citado en Barbour, 2013, p. 59).

Para ordenar la dinámica del grupo de discusión se diseñó una guía en la que se dispuso, además de los objetivos que se perseguían con su aplicación, la inclusión de una serie de interrogantes con las que se buscó promover la participación de los docentes. Las preguntas propuestas abarcan dos grandes dimensiones: el uso didáctico de la placa micro:bit para la enseñanza de la Matemática, y la tecnología digital para la comprensión del contenido matemático, y de los procesos constitutivos de la resolución de problemas.

Dado el escenario actual de pandemia por el COVID-19 en que nos encontramos, fue necesario realizar la sesión con el grupo de discusión a través de una videoconferencia llevada adelante con el servicio de videotelefonía de Meet de Google. Para realizar el registro de la sesión, con el objetivo de su posterior reproducción para la recolección de la información, se pidió el consentimiento de los docentes que intervinieron del grupo, a quienes se les garantizó el mantenimiento del anonimato y la confidencialidad de la información recabada. La presente ha sido una de las precauciones éticas que se han tenido en cuenta para este estudio.

El instrumento diseñado fue validado mediante juicio de experto a través de tres especialistas: dos de ellos de dilatada trayectoria en la enseñanza de la Matemática de nuestro país y el restante es un experto a nivel nacional, tanto por sus competencias profesionales como por su producción en temas de educación mediadas con tecnología digital.

La sesión de trabajo fue de una hora y media y participaron ocho docentes de Enseñanza Media de instituciones públicas de Uruguay, tamaño del grupo aceptado en la investigación en educación ya que favorece una dinámica activa entre los integrantes del focus y predispone para la conversación y discusión (Ibáñez, 1992).

7.2Análisis documental

Esta técnica, a diferencia del grupo de discusión en la que los investigadores tuvieron un rol protagónico en la obtención y registro de datos, permitió ampliar las posibilidades de recoger información desde una nueva perspectiva que la enriqueció. Tal como lo señala Yuni y Urbano (2006), “amplía la captación de los significados que nos permiten mirar esa realidad desde una perspectiva más global y holística” (p. 100).

Los documentos a los que hemos accedido para este estudio provienen de las producciones de los profesores para resolver la situación problemática planteada (Reto 3) durante la actividad Encuentro Matemático 2020, por lo que son documentos reales, y que se encuentran en diferentes soportes y formatos y su utilización, aunque generados a partir de la organización del Centro CEIBAL de la citada actividad, son de naturaleza pública. Por tanto, de acuerdo con lo señalado por Yuni y Urbano (2006), la intencionalidad de su elaboración es pública, son reales y presentados en formato visual y audiovisual.

La ficha utilizada para el análisis documental fue piloteada a través de cinco docentes que tienen formación similar a los que participaron del estudio pero que no participaron de él, a efectos de asegurar su fiabilidad.

8.  Procedimiento y análisis

La estrategia llevada a cabo para el análisis de los datos provenientes del grupo de discusión se elaboró siguiendo las recomendaciones de Glaser y Strauss (1967), a partir del diseño de dos tipologías de categorías, apriorísticas y emergentes. Así es que los significados que los docentes les atribuyen a aquellos aspectos concernientes a la integración de la tecnología digital a sus prácticas de enseñanza, al uso de la tecnología digital, en particular la placa micro:bit, para la mejora de la enseñanza de la Matemática, el uso de la placa micro:bit como un medio para la promoción del desarrollo de habilidades digitales y competencias de la Matemática, se agruparon en matrices de contenido que permitieron clasificar los datos emergentes (Miles y Huberman, 1984). Finalmente, los datos constitutivos de ambas categorías se triangularon con la información que provino del análisis documental con el objetivo de alcanzar mayor validez y consistencia en el análisis (Arias, 2000).

La Tabla 3 muestra un resumen descriptivo de las características generales de los documentos y sus singularidades.

Tabla 3: Identificación y características generales del material recogido

Código	Conocimiento matemático	Proceso que promovió la placa
Código	Conocimiento matemático	Proceso que promovió la placa
D1	Variable. Modelo 3UV para la comprensión de los aspectos que representan a una variable. Expresiones algebraicas.	Interpretación y significación del concepto de variable. Conjeturación. Generalización y justificación. Abstracción.
D2	Expresiones algebraicas	Algoritmia
D3	Variable	Validación. Los estudiantes buscan validar sus respuestas de manera intrínseca al problema.
D4	Variable. Relación de orden	Investigación
D5	Variable y uso de paréntesis	Trabajo en equipo
D6	Orden numérico	Etapas de la resolución de problemas. Trabajo colaborativo.
D7	Variable Expresiones algebraicas	Etapas de la resolución de problemas
D8	Variable. Relación de orden	Pensamiento computacional
D9	Variable.	Interés por el aprendizaje
D10	Variable. Relación de orden	Método de exhaución. Revisión de solución obtenida.
D11	Variable	Trabajo colaborativo en un foro diseñado exclusivo para el problema.
D12	Variable. Relación de orden	Trabajo en equipo. Gran motivación por el aprendizaje
D13	Variable. Relación de orden. Paridad e imparidad. Divisibilidad	Variantes de problema propuesto.
D14	Relación de orden. Operaciones con enteros	Trabajo en equipo. Etapas de la resolución de problemas.

Fuente: Elaboración propia.

9.  Resultados

Para identificar el uso con sentido pedagógico de las tecnologías digitales que hacen los profesores de Matemática que participaron de este estudio, se realizó un análisis de los segmentos de discurso y respuestas que provienen del grupo de discusión. Se desarrolló un análisis recurrente de los significados de los fragmentos, buscando identificar regularidades discursivas, lo que nos condujo a la determinación de cuatro familias semánticas que conformaron las categorías teóricas para el análisis.

Producto de este proceso, las categorías que se determinaron son las siguientes: “Uso de tecnología digital incide favorablemente en la mejora de la enseñanza de la Matemática”, “Entornos de aprendizaje dinámicos”, “Aprendizajes relevantes que estimulan procesos cognitivos”, “Trabajo colaborativo”. La Tabla 4 recoge las características de cada categoría.

Tabla 4. Características de las categorías semánticas

Categorías	Características
Uso de tecnología digital incide favorablemente en la mejora de la enseñanza de la Matemática.	El docente integra recursos de la placa micro:bit como un elemento que colabora a transformar la práctica de enseñanza.
Entornos de aprendizaje dinámicos.	Se caracterizan por la interactividad entre los participantes, lo que hace posible un mayor grado de compromiso e implicación en las tareas.
Aprendizajes relevantes que estimulan procesos cognitivos.	Aprendizajes significativos. Vinculados a procesos de resolución de problemas.
Trabajo colaborativo.	Trabajo en duplas o grupos en los que los alumnos trabajan colaborativamente en la búsqueda de solucionar el problema.

Fuente: elaboración propia.

Varios de los testimonios recogidos durante el grupo de discusión coinciden al destacar que el uso de la placa micro:bit para trabajar en la situación problemática propuesta incidió favorablemente en la mejora de la comprensión de los conceptos matemáticos puestos en juego (variable, expresiones algebraicas, relaciones de orden, conjuntos numéricos). Asimismo, los docentes concuerdan en que las transformaciones que se activan durante la programación por bloques permiten promover procesos constitutivos para la resolución de problemas (argumentar, justificar, generalizar, buscar regularidades y patrones, abstraer, ensayar, explorar, experimentar y validar). Tal como lo expresan los participantes del grupo de discusión cuando relatan motivos que los han impulsado a utilizar esta tecnología digital.

“el trabajo con la placa les permite organizar lo que están pensando, escribirlo de alguna manera que funciona, la placa le permite organizar las ideas, equivocarse, les permitió el desarrollo del pensamiento lógico-matemático además de habilidades y competencias digitales” (D10).

“la placa implica seguir procesando el mismo problema, ayuda a la validación. Ellos ven donde está bien y donde está mal, ayuda a la visualización, ayuda a ver dónde está el error, no es uno que los está corrigiendo, es el mismo recurso que se los está mostrando” (D 9).

Otro de los aspectos señalados por los docentes con relación al uso de la placa micro:bit es la de favorecer un entorno de aprendizaje dinámico que colabora en el aprendizaje de los conocimientos matemáticos.

“el año pasado me pasó que los chiquilines al reto lo deshicieron y lo rehicieron como quisieron ellos. Justo estábamos trabajando con números enteros (…) y ellos dijeron – vamos a hacerlo para los números enteros, que aparezcan negativos y positivos, vamos a cambiarle el orden de los botones-. Lo hicieron de ellos, eso me pareció super importante, tomaron el reto, lo convirtieron y lo hicieron suyo” (D10).

Son elocuentes las manifestaciones que señalan, el hecho de incorporar la placa micro:bit a las prácticas de enseñanza promueve aprendizajes significativos y estimula procesos cognitivos que permiten reconocer diferentes significados de un objeto matemático, para en una etapa ulterior establecer relaciones entre estas representaciones. Asimismo, el uso de la placa promueve habilidades para formular, representar y resolver situaciones problemáticas nuevas.

“con esto de la programación ellos tienen que ver que funcione tienen que justificar, entonces ayuda a que entiendan por qué es importante justificar y que eso se traslade a la matemática a justificar los razonamientos de ellos” (D14)

“lo interesante de la placa, es cuando la programación no les funciona porque ahí es justamente cuando ellos tienen que volver al principio y en descomponer cada paso, creo que en ese momento entienden la importancia de justificar, argumentar, ir pensando, esa metacognición por decirlo de alguna manera, de pensar cómo hicieron cada cosa” (D11).

Destaca también la posibilidad de desarrollar estrategias de interacción social en las que los alumnos trabajan en grupos persiguiendo una meta en común. El centro de estas actividades es el alumno y el docente es un facilitador y guía del aprendizaje. En este sentido la placa micro:bit para la resolución del problema motiva a los alumnos y los predispone para una participación de su aprendizaje.

“los noté más confiados, agarraron más confianza en sí mismos, varios de los que decían -la matemática a mí no me gusta-, -yo no sé- o -yo no puedo- a partir de ese reto, vieron que pudieron, y que había compañeros que no habían podido tan rápido como ellos, los noté más abiertos a otras instancias dentro de la matemática” (D4).

En los relatos, uno de los temas que aparece primero en casi todos los participantes, hace referencia a la motivación que genera el uso de la placa en las aulas. Los docentes asocian, y lo explicitan, cambios en cuanto a la actitud frente al aprendizaje de la asignatura y en general hacia otro tipo de aprendizajes.

“vi un cambio en la relación grupal, mucho intercambio entre ellos, quisieron contar la experiencia, se sintieron fortalecidos y quisieron salir a mostrar lo que habían hecho. Yo si les doy un problema matemático no hubieran querido salir a mostrar y decir mira qué lindo mi problema” (D3).

“creo que una de las huellas que dejó el uso de la placa es que ellos reconozcan que uno no sabe todo, (...) ellos creen que nosotros tenemos que saber todo. El docente acompaña el proceso” (D5).

A partir de las evidencias recolectadas en el grupo de discusión se realizó otro análisis que permitió identificar varios testimonios, que van en la misma dirección que lo anteriormente planteado, respecto a las prácticas de enseñanza mediadas con tecnología digital. Esta praxis pedagógica fue asociada con los procesos de modificación y redefinición, Puentedura (2006) ambos constitutivos de la transformación de los procesos de enseñanza.

“los noté más confiados, a partir de ese reto, que vieron que pudieron, los noté más abiertos a otras instancias dentro de la matemática noté un cambio de actitud en la disciplina, querían que los sorprendiera, me pusieron la vara alta, porque querían siempre que los sorprendiera” (D4).

En el siguiente apartado vamos a presentar los resultados de los análisis desarrollados a un conjunto de diversos documentos que son la evidencia empírica y sirven como testimonio de los procesos de resolución de las actividades y de los conocimientos matemáticos involucrados en ellas.

En primera instancia se buscó organizar los documentos en una matriz de datos de modo de obtener una descripción general del contenido de dichos documentos, para en una segunda instancia desagregar el contenido según sus singularidades con el fin de analizar la forma en que los docentes de Matemática utilizaron la placa micro:bit para la resolución de la situación problemática propuesta. Este proceso nos condujo a cuatro categorías de análisis: “Habilidades y competencias matemáticas”, “Conocimiento matemático para la resolución de la situación”, “Trabajo en equipo” y “Habilidades digitales”

9.1 Evidencias asociadas a las “Habilidades y competencias matemáticas“

En las propuestas de resolución de los profesores se evidencian una serie de habilidades y competencias matemáticas útiles para el abordaje de la actividad. Si bien las características de la situación propuesta son propicias para que los alumnos puedan desarrollar procesos de exploración, experimentación, descomposición del problema en otros problemas de menor complejidad, justificación, argumentación, validación y modelación, son elocuentes algunos relatos que los docentes escribieron en la plataforma CREA en este sentido.

9.2 Proceso de validación

“Hoy terminamos el reto N°3 y quedó probado en las micro:bit” (D3).

Figura 1. Programación de la placa micro:bit - Docente 3

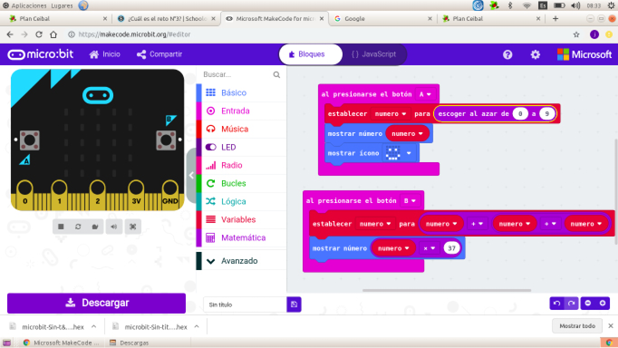
Fuente: elaboración propia.

A través del comentario de esta docente, queda de manifiesto cómo los estudiantes buscan la validación a sus respuestas de manera intrínseca al problema, y no necesariamente en su docente. La tarea de testear programas es de hecho parte fundamental en la programación y, en el sentido descrito anteriormente, trasciende y es fundamental también en el quehacer matemático. Su equivalente en la resolución de problemas es la instancia de examinar la solución obtenida, paso clave y concluyente según Pólya (1989).

9.3Múltiples caminos de resolución

“nos fue muy bien en este reto, se coparon bastante y encontraron caminos distintos que ni yo había pensado, lo cual me parece muy bueno. Comparto con ustedes un videíto del trabajo pero también nos filmamos en la radio” (D5)

Aparece en la relatoría de la docente una característica que consideramos natural al programar y es que no existe un camino único de resolución. Muchas veces se asocia la matemática a métodos de resolución únicos e indiscutibles, pero el haberla abordado a través del desarrollo de un programa, deja explícito para los estudiantes que se puede resolver un problema siguiendo caminos diferentes.

9.4Método de exhaución

“en un subgrupo trabajaron con un montón de iconos diferentes para indicar el resultado correcto y el error, tics, caritas felices, corazones etc. Y además les surgió la duda de que pasa si justo se nos mostraban dos números iguales, por lo que decidieron agregar una condición más, que si los números eran iguales, había que apretar ambos botones a la vez para que la placa lo indicara como correcto” (D10).

Este comentario evidencia cómo el diseño de un programa relativamente sencillo conduce a que los estudiantes deban realizar análisis por exhaución de una manera que surge como una necesidad del juego. A su vez, esta necesidad surge de examinar la solución obtenida, un paso que muchas veces los estudiantes omiten.

Figura 2. Programación de la placa micro:bit - Docente 10

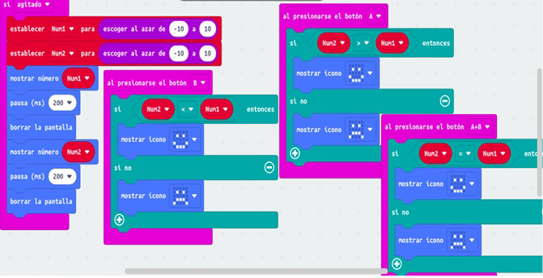
Fuente: Elaboración propia.

9.5Experimentar

“Probamos varias ideas pero la enviada es una utilizando Enteros. Este trabajo además de ser en coordinación con la docente de informática también tuvo la participación del laboratorio Ceilab en una experiencia con alumnos de 6tos de primaria” (D7).

Aunque el foco del reto no se encontraba en los distintos conjuntos numéricos, resultó interesante observar cómo la actividad obró como disparador para trabajar con ellos, aprovechándose el programa y haciendo cambios sencillos al mismo para probar distintas alternativas dependiendo del conjunto numérico utilizado. De este modo se logró trabajar en la clase de Matemática como un laboratorio, no solo en lo que respecta al uso del laboratorio Ceilab como entorno físico, sino principalmente a la modalidad de trabajo descrita por la docente en torno a la actividad planteada.

9.6Evidencias asociadas al “Conocimiento matemático”

“En el día de hoy terminamos con el desafío 3 con (…) el Liceo de Capilla del Sauce-Florida. Trabajaron con reducción de la expresión algebraica y realizaron conclusiones excelentes” (D1).

Figura 3. Visualización de la programación en el sitio Makecode y placa micro:bit	Figura 4. Resolución del problema - Docente 1

Fuente: Elaboración propia.

Los estudiantes, en conjunto con su docente, lograron significar el concepto de variable a partir de casos particulares para luego formalizarlo. Se logra así, a través de la práctica, introducir una forma de pensamiento más abstracta. Además de utilizar una variable como número general y en relación funcional, operaron con expresiones algebraicas.

Un aspecto relevante de la programación por bloques es el correcto anidamiento de estos. Su equivalente matemático, que es más notorio cuando los bloques están asociados a operaciones aritméticas, son los paréntesis. Aquí, si los bloques {} + {} (repetido tres veces) y {} × {} se hubieran “encastrado” de otra manera, el resultado no hubiera sido el esperado, equivalentemente a si se cambia el lugar de los paréntesis en una expresión matemática. Una de las diferencias es que, si se diera un error en el anidamiento de los bloques, el propio programa lo evidenciaría al ser testeado, no obteniéndose lo esperado.

Este aspecto queda claramente marcado en el trabajo presentado por la docente D5 en el siguiente enlace https://makecode.microbit.org/49715-29332-08333-75022

La evidencia que sigue muestra cómo el problema fue resignificado por el docente y sus alumnos.

“Hemos trabajado con el profesor de informática donde los alumnos realizaron algunas variantes, crearon una variable mayor-menor para tres números. Hicieron el Código para par e impar también” (D13).

Una vez más, tomando como base una programación relativamente sencilla, lograron realizar adaptaciones que se consideraron interesantes y oportunas. Las mismas siguieron la línea del trabajo en torno al mismo concepto matemático (orden) y otros (divisibilidad). Así, la potencialidad de usar la programación en la clase de matemática se ve reflejada en las palabras del docente.

9.7Evidencias asociadas al “Trabajo en equipo”

Si bien no se explicita como uno de los requisitos de la actividad, observamos cómo naturalmente se abordó a través del trabajo en equipo. Este aspecto es tan importante en la programación como en la Matemática, y propiciar de manera natural y productiva este tipo de trabajo constituye uno de los objetivos del Encuentro Matemático y de la Educación misma.

Figura 5. Trabajo en equipo - Docente 4

Fuente: elaboración propia.

“Logramos concluir con el reto 3. Nos costó, probamos y probamos hasta que se logró, investigaron sobre el programa porque no lo conocían. Algunas fotos del trabajo en equipo” (D4).

“estamos participando con alumnos de primer año, algunos de ellos en la escuela habían trabajado con micro:bit, pero en su mayoría esta es la primera experiencia. Como en todo grupo hay alumnos muy motivados que están buscando las respuestas y la mandan por WhatsApp a los demás. Mañana viernes haremos la puesta en común de lo que hemos logrado y lo comparto por acá, también fotos de ellos trabajando” (D7).

https://drive.google.com/file/d/1TkoG9aLhQA_qs8L07ArUdnPm69OGMocF/view?usp=sharing

La actividad también posibilitó un cambio en los roles, en este caso la docente se mostró receptiva a aprender de sus alumnos.

“En el momento de plantear la actividad, los alumnos me comentaban que algunos ya habían trabajado en la escuela con la placa así que hicieron duplas con los que no la conocían para hacer la programación, comenzamos en el simulador. Yo no había trabajado con micro:bit así que les dije que serían mis profes, ... En este reto vi mucho trabajo en equipo y como se ayudaban los alumnos entre sí para lograr hacer la actividad, hubo más motivación, solidaridad” (D12).

https://drive.google.com/file/d/1vBZE3zXjA8skP0qwZ2n0MsVvR3jXm1ys/view?usp=sharing

Así, el rol de la docente se desdobla como guía para ciertos momentos didácticos, y como aprendiz en otros. Esto fortalece vínculos y de hecho es algo que se explicita en su relato.

Por otra parte, el poder pensar el reto bajo una doble dimensión en cuanto a habilidades involucradas (matemática - programación), permitió formar duplas con sentido, teniendo un motivo para elegir sus integrantes, donde cada estudiante pudo complementar a su compañero o compañera de equipo.

9.8Evidencias que dan cuenta de las “Habilidades digitales”

Si bien consideramos que varios de los ejemplos propuestos en las demás categorías son señal elocuente de las habilidades digitales de los docentes, quisimos señalar otras que por su singularidad no están incluidas en las otras categorías.

“comenzaron a crear el juego, el mismo dura 60 segundos, si contestan bien, el juego les brinda un punto y si contestan mal, el juego les resta un punto. Para crear el juego, retomaron lo trabajado en el curso del año anterior: pensamiento computacional. En este grupo, están acostumbrados a trabajar con la micro:bit, dado que tienen una sala de robótica en dicha institución” (D8).

Propuesta entregada por la docente: https://makecode.microbit.org/_FuR9tPJPh08M

10.Discusión y conclusiones

A través de los testimonios de los docentes, que han participado del estudio, se ha podido constatar que el uso que ellos hacen de placa micro:bit para llevar adelante actividades como la propuesta en el Reto 3 del concurso, Encuentro Matemático permite transformar y mejorar las prácticas de enseñanza.

Estos docentes concuerdan que el uso de la placa micro:bit posibilitó mejorar la comprensión de conceptos matemáticos como variable, relaciones de orden, divisibilidad, conjuntos numéricos, entre otros presentes en la actividad propuesta. Así mismo entienden que posibilitó la promoción de una gran variedad de procesos constitutivos de la resolución de problemas como: exploración, experimentación, descomposición, justificación, argumentación, validación, abstracción y modelación. Pero también esta tecnología digital les ha permitido estimular el interés y la motivación de los alumnos por el aprendizaje, la creatividad, y ha sido fuente de promoción del trabajo colaborativo y las interacciones sociales. Los señalamientos que los docentes hacen en el focus nos permitieron determinar cuatro categorías: “Uso de tecnología digital incide favorablemente en la mejora de la enseñanza de la Matemática”, “Entornos de aprendizaje dinámicos”, “Aprendizajes relevantes que estimulan procesos cognitivos”, “Trabajo colaborativo” que se refuerzan a partir de la revisión documental de las actividades proporcionadas por los docentes.

Las evidencias documentales que hemos podido recoger, en la plataforma CREA, son elocuentes respecto a los usos transformadores, Puentedura (2006), que ofrece la programación de la placa micro:bit como una forma de organizar las actividades pedagógicas de una manera innovadora que sería imposible de realizar si no se dispusiera de una tecnología digital con las singularidades de este recurso.

La incorporación de la tecnología por sí sola no genera cambio en los aprendizajes, ya que si bien tiene el potencial para realizarlo no es suficiente para concretarlo. La transformación se concreta con el acompañamiento de la tecnología digital con sugerencias y orientaciones técnico-pedagógicas que hacen al cambio metodológico y que determinan el uso que se da a estás en los ámbitos educativos. Este aspecto se materializa en las propuestas que se enviaron a los docentes, que además de contener propuesta de la situación problemática, fueron acompañadas de una serie de materiales escritos y audiovisuales conteniendo sugerencias y orientaciones metodológicas, específicamente, de cómo utilizar la placa micro:bit y algunas pautas para su incorporación en la resolución del problema.

La evidencia señaló que además de estos materiales, la forma en que cada docente organizó el trabajo con sus alumnos y los procesos de construcción conjunta que se han desplegado, “redefinen” los procedimientos de las guías preestablecidas. Es justamente en estas interacciones entre los participantes y en esta redefinición de procesos, que además se nutre de: conocimientos previos, expectativas, motivación y el contexto, donde la tecnología digital cobra un sentido pedagógico. Este hallazgo es coincidente con algunos estudios internacionales (Coll, Onrubia y Mauri, 2007; Coll, 2004) sobre la capacidad de transformación y mejora de las prácticas de enseñanza de la Matemática mediadas con tecnología digital.

Los hallazgos de este estudio deben ser interpretados teniendo en cuenta las posibles limitaciones propias del enfoque utilizado. Vemos conveniente para futuros trabajos utilizar un enfoque mixto que permita contrastar y potenciar los hallazgos con resultados que provengan tanto de estudios cualitativos como cuantitativos.

Referencias

Arias, M. (2000). La triangulación metodológica: sus principios, alcances y limitaciones. Disponible en https://bit.ly/3h5LG7z

Attard, C. (2015). Introducing iPads into primary mathematics classrooms: teachers’ experiences and pedagogies. In: Meletiou Mavrotheris, M, Mavrou K.; Paparistodemou, E. (org.). Integrating touch enabled and mobile devices into contemporary mathematics education (pp. 197-217). Hershey: IGI Global.

Bansilal, S. (2015). Exploring student teachers’ perceptions of the influence of technology in learning and teaching mathematics. South African Journal of Education, Pretoria, 35(4), 1-8. https://doi.org/10.15700/saje.v35n4a1217 

Barbour, R. (2013). Los grupos de discusión en Investigación Cualitativa. Madrid: Morata.

Coll, C. (2004). Los usos de las TIC en los procesos formales y escolares de enseñanza y aprendizaje. Revista Tecnología y Prácticas Educativas, 25, 17-19.

Coll, C., J. Onrubia, y T. Mauri, T. (2007). Tecnología y prácticas pedagógicas: las TIC como instrumentos de mediación de la actividad conjunta de profesores y estudiantes, Anuario de Psicología, 38(3), 377-400.

Dussel, I. (2011). Aprender y enseñar en la cultura digital. VII Foro Latinoamericano de Educación TIC y educación: experiencias y aplicaciones en el aula. Disponible en https://bit.ly/2WQoTpz

García-González, L. y Solano-Suarez, A. (2020). Enseñanza de la Matemática mediada por la tecnología. EduSol, 20(70), 84-99. Disponible en https://bit.ly/38FUInc

Glaser, B. y Strauss, A. (1967). The discovery of grounded theory. Chicago: Aldine Press.

Goehle, G. y Wagman, J. (2016). The impact of gamification in web based homework. Problems, Resources, and Issues in Mathematics Undergraduate Studies, 26(6), 557- 569. https://doi.org/10.1080/10511970.2015.1122690

Ibáñez, J. (1992). Más allá de la sociología. El grupo de discusión. Teoría y crítica. Siglo XXI, Madrid.

Korma, R. (2005). Monitoring and Evaluation of ICT for Education Impact: A Review. In Wagner, D., Day, B., James, T., Kozma, R., Miller, J., and Unwin, T. (Eds.). Monitoring and evaluation of ICT in education projects: A handbook for developing countries, (pp. 11-20). Washington, D.C.: The World Bank.

Miles, M. y Huberman A. (1984). Qualitative data analysis. A source book of new methods, Beverly Hills, Sage

Pecharromán, C. (2014). El aprendizaje y la comprensión de los objetos matemáticos desde una perspectiva ontológica. Educación matemática, 26(2), 111-133. Recuperado de https://bit.ly/2WX94wD

Pólya G. (1989). Cómo plantear y Resolver problemas. México. Editorial Trillas

Puentedura, R. (2006). Transformation, technology, and education [Audio en podcast]. Recuperado de http://hippasus.com/resources/tte/

Revelo, J. (2017). Modelo de integración de la competencia digital docente en la enseñanza de la matemática en la universidad tecnológica equinoccial. (Doctoral dissertation). Universidad de Extremadura. Recuperado de https://bit.ly/3h3ncfi

Rivera-Vargas P. y Cobo-Romani C. (2020). Digital learning: distraction or default for the future. Digital Education Review, 37. http://greav.ub.edu/der/

Sosa, M. (2015). El proceso de integración de las tecnologías de la información y comunicación en centros de Educación Primaria: Estudio de caso múltiple (Tesis Doctorado). Departamento de Ciencias de la Educación. Universidad de Extremadura, Cáceres. Recuperado de https://bit.ly/3tj3qB5

Tedesco, J. (2012) “Educación y Justicia social en América Latina “. Buenos Aires.

Vaillant, D., Rodríguez-Zidán, E. y Bentancor-Biagas, G. (2020). Uso de plataformas y herramientas digitales para la enseñanza de la Matemática. Ensaio: Avaliação e Políticas Públicas em Educação, 28(108), 718-740. https://doi.org/10.1590/S0104-40362020002802241

Vaillant, D. (2015). Prólogo. En “Educación y tecnología en el Uruguay: Una mirada desde la investigación” Recuperado de https://bit.ly/3yOisQL

Valiente, O. (2010). 1-1 in Education: Current Practice, International Comparative Research Evidence and Policy Implications. OECD Education Working Papers, 44.

Yuni, J. y Urbano, C. (2006). Técnicas para investigar 2. Recursos metodológicos para la preparación de proyectos de investigación: Córdoba: Brujas.