Género y rendimiento escolar en América Latina. Los datos del SERCE en matemática y lectura

* Profesor titular, docente investigador. Director de la Maestría en Educación. Universidad Nacional de Quilmes.
** Profesora. Universidad Nacional de Quilmes.
*** Profesora. Universidad Nacional de Quilmes.

SÍNTESIS: Utilizando los datos del Segundo Estudio Regional Comparativo y Explicativo (serce), llevado a cabo por la unesco en América Latina, este trabajo investiga la asociación entre género y logro en matemática y en lectura, en la educación primaria (efecto género). Se estudia el efecto del nivel socioeconómico del alumno y de la escuela, y su interacción con la desigualdad entre géneros, y se analiza también la variabilidad del efecto género entre los países participantes, para lo cual se utilizan modelos multinivel bivariados.

Los resultados revelan que los niños se desempeñaron significativamente mejor en matemática, mientras que las niñas obtienen mejores resultados en lectura, incluso cuando el nivel socioeconómico es «controlado». En cuanto al tamaño de estas brechas de género, se advierte que varía de país a país, con mayor intensidad que en los países desarrollados. Por un lado, los países con alta disparidad en matemática también presentan una alta desigualdad en lectura. Además, las niñas son más afectadas que los niños por las condiciones socioeconómicas. En lectura, la situación es diferente según el contexto sociocultural de la escuela. Estos resultados empíricos sugieren que las cuestiones de género en el aprendizaje escolar deben ser incluidas en la agenda política de los países de América Latina.

Palabras clave:rendimiento escolar | género | América Latina | educación primaria | análisis multinivel.

Gênero e rendimento escolar na América Latina. Os dados do SERCE de Matemática e Leitura

Síntese: Utilizando os dados do Segundo Estudo Regional Comparativo e Explicativo (serce), levado a cabo pela unesco, na América Latina, este trabalho estuda a associação entre gênero e conquistas em Matemática e em Leitura, na Educação Primária (efeito gênero). Estuda-se o efeito do nível socioeconômico do aluno e da escola, e sua interação com a desigualdade entre gêneros e se analisa também a variabilidade do efeito gênero entre os países participantes, para o qual se utilizam modelos multinível bivariados.

Os resultados revelam que os meninos tiveram, significativamente, melhor desempenho em Matemática, enquanto as meninas obtiveram melhores resultados em Leitura, inclusive quando o nível socioeconômico é «controlado». Quanto ao tamanho dessas brechas de gênero, adverte-se que varia de país para país, com maior intensidade do que nos países desenvolvidos. Por outro lado, os países com alta disparidade em Matemática também apresentam uma alta desigualdade em Leitura. Ademais, as meninas se veem mais afetadas pelas condições socioeconômicas do que os meninos. Em Leitura, a situação é diferente, dependendo do contexto sociocultural da escola. Estes resultados empíricos sugerem que as questões de gênero na aprendizagem escolar devem estar incluídas na agenda política dos países da América Latina.

Palavras-chave: rendimento escolar | gênero | América Latina | Ensino Primário | análise multinível.

Gender and school performance in Latin America. Serce details in math’s and reading

Abstract: Using data from the Second Regional Comparative and Explanatory Study (serce) conducted by unesco in Latin America, this paper investigates the association between gender and achievement in math’s and reading in Primary Education (gender effect). So, the effect of socioeconomic status of the student and the school, and their interaction with gender inequality is studied, and the effect of gender variability among participating countries is also analyzed, for which bivariate multilevel models are used.

The results show that children performed significantly better in math, while girls score higher on reading, even when socioeconomic status is «controlled». Regarding to the size of these gender gaps, it is noted that varies from country to country, with greater intensity than in developed countries. On the one hand, countries with high disparity in math also have high inequality in reading. In addition, girls are more affected than boys by the socioeconomic conditions. In the case of reading, the situation is different according to the sociocultural context of the school. These empirical results suggest that gender issues in school learning should be included in the political agenda of the countries of Latin America.

Keywords: rschool performance | gender | Latin America | Primary Education | multilevel analisys.

La igualdad de oportunidad para todos es un valor central en la sociedad democrática, y supone que el ascenso en la estructura social no debería estar afectado por variables tales como el origen social, el género y la etnia. El sistema educativo juega un papel muy importante en la distribución de las oportunidades futuras, no solo por sus certificaciones sino también por el nivel de aprendizaje efectivamente logrado por el alumno. Diversas investigaciones han reportado la existencia de altas tasas de retorno de los puntajes medidos con test de logro cognitivo sobre la educación (Bishop, 1992; Boissiere y otros, 1985; Currie y Duncan, 2001; Murnane y otros, 1995; Rivera-Batiz, 1992). Por tanto, los resultados en los tests cognitivos son predictores ajustados de futuras posibilidades económicas. Por ello, la intensidad de la correlación entre origen social o género, por un lado, y el desempeño escolar del alumno, por el otro, es un indicador inequívoco del grado de inequidad educativa, violación del principio de igualdad de oportunidades.

En este artículo se investiga la desigualdad de género en los logros de matemática y de lectura en la educación primaria de algunos países de América Latina, poniendo especial atención en sus interacciones con el origen socioeconómico del alumno y con la composición socioeconómica de la escuela. Se analizan los datos del Segundo Estudio Regional Comparativo y Explicativo (serce) realizado por el Laboratorio Latinoamericano de Evaluación de la Calidad de la Educación (llece) de la orealc/unesco.

Las diferencias de género en los resultados de pruebas de aprendizaje han sido objeto de numerosas investigaciones. Sobre la base de varios estados del arte (Hyde y Linn, 1986; Wilder y Powell, 1989; Willingham y Cole, 1997), la idea de que los niños rinden menos que las niñas en lectura pero mejor en matemática ha sido predominante, aunque persisten desacuerdos acerca de la edad en que ello emerge (Leahey y Guo, 2001), si varía según sea la medición del logro (Tsui, 2007; Won, Lam y Ho, 2002), si se ha reducido o se ha mantenido estable (Hedges y Nowell, 1995).

Las evaluaciones internacionales (timss, pirls, pisa) han permitido la elaboración de numerosos estudios comparativos entre países. En general, y con algunas variaciones, han confirmado la existencia de diferencias de género en lectura y matemática en la mayoría de los países participantes. Con datos del pirls 2006, Mullis y otros (2007) concluyeron que en todos los países participantes, las niñas de 4.º y 8.º lograban un rendimiento en lectura significativamente mejor que el alcanzado por los niños. En matemática, los resultados fueron más diversos. De los 43 países que participaron en timss 2007, las niñas de 4.º se desempeñaron significativamente mejor que los niños en ocho países, y los chicos lo hicieron mejor en 16 países, mientras que en 8.º estos resultados se invirtieron. En 1995, sin embargo, en ninguno de los países el desempeño de las niñas en matemática había sido superior al de los chicos (Mullis y otros, 2005).

En América Latina, los resultados de la evaluación realizada por el llece en 1997 (llece, 2001), mostraron que en lectura las alumnas de 4.º obtuvieron mejores resultados que los varones en nueve de los 12 países participantes, mientras que en matemática los varones superaban a las niñas en cinco países. Según el serce 2007, las niñas superaron a los niños en lectura en seis países, mientras que en matemática los niños tuvieron un mejor desempeño en 11 países (llece, 2008).

También se han realizado diversos análisis nacionales sobre las diferencias de género. En Brasil, Nicaragua y Honduras, encontraron que los niños entre 4.º y 6.º se desempeñan más pobremente que las niñas en la lectura, pero obtienen mejores puntuaciones en matemática (Franco y otros, 2007; Universidad Pedagógica Nacional,1998); en México, la brecha de género no fue significativa en lectura, pero los niños se desempeñaron mejor en matemática (Blanco, 2008); en Costa Rica y Perú no hubo diferencias significativas en ambas disciplinas (iimec, 1997; Ministerio de Educación de Perú, 2001); en Bolivia, Uruguay y Paraguay (doee; 1998; Fernández, 2002; simecal, 1998) la brecha de género no fue significativa en lectura. En Argentina, las niñas obtuvieron mejores resultados en lectura, y no hubo diferencia de género significativa en matemática en 3.º y 6.º (Cervini, 2010).

Algunos resultados no son consistentes con los del llece debido, en parte, a los niveles de significación estadística adoptados. De cualquier manera, los datos indicarían variación de la brecha de género entre los países.

Menos frecuentes han sido los estudios que han abordado la interacción entre el efecto género y el nivel socioeconómico de la familia del alumno y/o de la escuela. Se ha constatado no solo que las diferencias de rendimiento entre niños y niñas son mayores en los grupos socioeconómicos más bajos (Cuttance y Thompson, 2008) sino que, además, el nivel socioeconómico del vecindario (contexto) tiene efecto negativo significativo sobre la brecha de sexo en la habilidad en matemática (Hinshaw, 1992), donde el efecto barrio es mayor para los varones que para las niñas (Entwisle, Alexander y Olson, 1994).

En lectura, «el estatus socioeconómico más alto mejora el rendimiento de los niños en relación con el de las niñas» (Buckingham, 1999, p. 8), lo que implica que el nivel socioeconómico afecta a la brecha de género, ampliándola o reduciéndola. Cuando aparece la brecha de género en la lectura, esta solo afecta a los niños de familias pobres (Entwisle y otros, 2007). Con base en los datos de pisa relativos a una mayoría países desarrollados, Marks (2008) encontró que no existen diferencias significativas entre géneros respecto del efecto de la situación socioeconómica familiar.

En América Latina, ninguno de los informes del llece ha analizado las brechas de género en detalle. La significación estadística de la variación interpaíses del efecto de género, y las interacciones de tales efectos con los niveles socioeconómico familiar y de la escuela, han estado ausentes. En este trabajo se pretende llenar estas lagunas de conocimiento.

Al encarar este trabajo no hemos propuesto como objetivo determinar los siguientes puntos: a) si existen evidencias empíricas que sustenten las hipótesis del efecto género; b) la variación entre países y escuelas, y c) la interacción con los niveles socioeconómicos del alumno y de la escuela.

Tal objetivo puede ser desglosado en las siguientes preguntas de investigación:

Se analizan los datos del serce, cuya descripción completa se encuentra en llece (2008). Se consideran los resultados de las pruebas de matemática y de lectura, y datos provenientes de los cuestionarios del alumno y de su familia. Para la conformación de la base de datos se han seguido los criterios expuestos en otro trabajo (Cervini, 2012). La base analizada consta de 89.944 alumnos en 2443 escuelas de 16 países y del Estado de Nuevo León (México).

Las variables dependientes son los puntajes (rendimiento) obtenidos por el alumno en las pruebas de matemática y de lectura desarrolladas y aplicadas por el serce. Las variables independientesson:

El género (fem) se trata como variable dummy. Todas las otras variables independientes son centradas en la gran media. El efecto contextual es capturado por «variables de composición», las cuales «miden un aspecto de la composición de la escuela a la que el estudiante individual asiste» (Goldstein, 1995, p. 30). Al incluir la variable correspondiente del nivel alumno, el efecto contextual expresa el impacto de la composición estudiantil de la escuela en el rendimiento individual, adicional a la influencia directa de la variable individual.

Los datos del serce son analizados con modelos multinivel bivariados (Goldstein, 1995), recomendado cuando se trata de datos anidados jerárquicamente (alumno, escuela, país) y se pretende investigar de manera simultánea dos variables-respuestas (puntajes en matemática y en lectura). Cada una de ellas es parte de un sistema único de ecuaciones, a través del cual se estiman las correlaciones entre ellas y de ellas con cada uno de los factores exógenos.

Una de las ventajas del modelo bivariado es que permite recuperar los missing en una de las variables-criterio a través de la imputación directa por regresión de la otra variable dependiente, y viceversa. Los modelos están compuestos por una parte fija y una parte aleatoria. En la primera se encuentran los parámetros que expresan las relaciones entre el rendimiento y los factores considerados. Cuando los predictores son categoriales (por ejemplo, género), los modelos estiman las distancias promedios entre categorías. En la parte aleatoria se estima la variación de los parámetros en cada nivel de agregación. En el presente caso, el interés se centra en la variación de los coeficientes de fem de cada país en torno a la distancia promedio del conjunto de países.

Los pasos del análisis son los siguientes: estimación de las medias globales de ambas disciplinas y la descomposición de la varianza total; estimación del efecto del género sin y con «control» del nivel socioeconómico del alumno y de la escuela; el efecto interactivo del género, y, finalmente, el análisis de aleatoriedad de tal efecto.

Se estiman las medias globales y las descomposiciones proporcionales de las varianzas de ambas materias. En la parte fija, los resultados son:

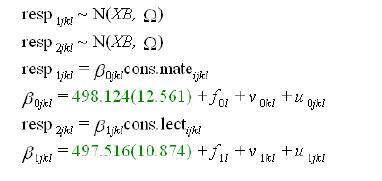
donde resp1jkl refiere al puntaje de matemática del alumno j, en la escuela k del país l; resp2jkl refiere al puntaje de lectura, con similar denotación para los tres niveles; cons.mate es una constante = 1 para cada puntaje de matemática, yβ0jkl es un parámetro asociado a cons.mate, compuesto por el logro promedio estimado ß0(parte fija), y por ƒ0l, ν0kl y µ0jkl, «residuos» en los niveles país, escuela y alumno, respectivamente, o sea, cantidades aleatorias, no correlacionadas, normalmente distribuidas, con media = 0 y cuyas varianzas respectivas (s2ƒ0, s2ν0 y s2m0) han de estimarse; cons.lect se refiere a lectura, con los cambios correspondientes de denotación (β1jkl y ß1; «residuos»: ƒ1l, ν1kl y µ1jkl; varianzas a estimar: s2ƒ1,s 2ν1 y s2m1).

Ambos promedios (498,124 y 497,516) son muy similares y, a simple vista, el modelo es estadísticamente significativo (los errores estándar, entre paréntesis, son notablemente menores que las estimaciones correspondientes).

Los países difieren significativamente entre sí respecto del promedio alcanzado por sus alumnos, tanto en lectura (s2ƒ1 = 1988,057) como en matemática (s2ƒ0 = 2657,396). Estas variaciones representan el 21,65% (2657,396 / 12307.837*100) y 17,8% de la variación total en matemática y en lectura, respectivamente, y pueden interpretarse como «efecto bruto» del país sobre el nivel de rendimiento de los alumnos (coeficiente de correlación «intra-clase»).

De acuerdo a estas estimaciones, los países de la región son más homogéneos respecto de los resultados en lectura comparados con los de matemática.

Por otra parte, el peso relativo de las diferencias «entre escuela» dentro de los países respecto de matemática (2996,919 / 12307.837*100 = 24,4%) es levemente superior a la variación «inter-país» y muy similar a la de lectura (23,8%).

El término de covarianza en el nivel país (sƒ01 = 2130,725) es levemente superior al del nivel escuela (sν01 = 2480,177) respecto de las varianzas correspondientes. Con base en estas estimaciones es posible calcular los coeficientes de correlación entre los interceptos correspondientes. En el nivel escuela y país los coeficientes son positivos y notablemente altos (0,88 y 0,93, respectivamente). Entonces, a medida que sube el rendimiento en una disciplina, también sube en la otra. El rendimiento promedio de un país en matemática predice el rendimiento promedio obtenido en lectura. Si el rendimiento promedio de matemática está por arriba del promedio estimado para todos los países, ese país muy probablemente alcanzará un promedio en lectura que también estará por encima del promedio global de esa disciplina.

Al agregar la variable fem como predictor en la parte fija del modelo anterior, se obtienen los siguientes resultados:

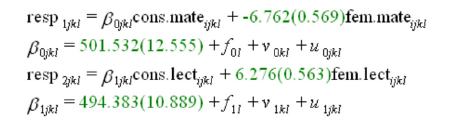
En promedio, el puntaje de las mujeres en lectura se distancia del obtenido por los varones en 6,276 puntos, mientras que en matemática la distancia (-6,762) es a favor de los varones. Ambas distancias son similares en magnitud relativa. El modelo es altamente significativo (prob. £ 0.001) y, por tanto, puede afirmarse que el género afecta la distribución de los aprendizajes en ambas disciplinas, y con la misma intensidad.

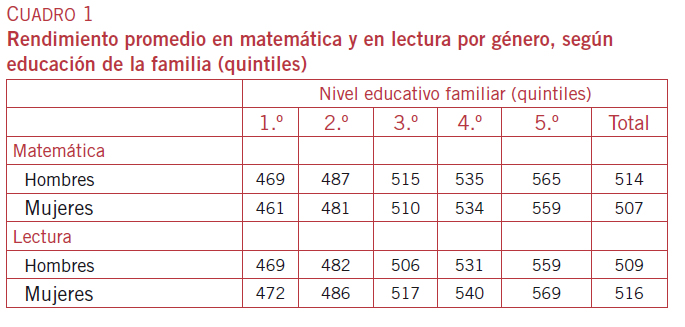
En el cuadro 1 se exhiben los rendimientos promedio de varones y mujeres pertenecientes a distintos niveles (quintiles) de educación de los padres.

En primer lugar, se constata que el mejor desempeño de los varones en matemática respecto de las mujeres en general, no se sostiene si se considera el indicador de nivel cultural familiar. El promedio de las mujeres en un quintil dado siempre es superior al promedio de los varones en el quintil inmediato inferior. Así, por ejemplo, las mujeres en el segundo quintil obtienen un rendimiento promedio en matemática (481) superior al obtenido por los varones situados en el primer quintil de ese indicador (469). De la misma forma se comporta la inferioridad de los hombres en lectura.

En segundo lugar, la ventaja de los varones en matemática se mantiene en todos los quintiles de nivel educativo familiar, comportamiento que también se verifica con el predominio de las mujeres en lectura.

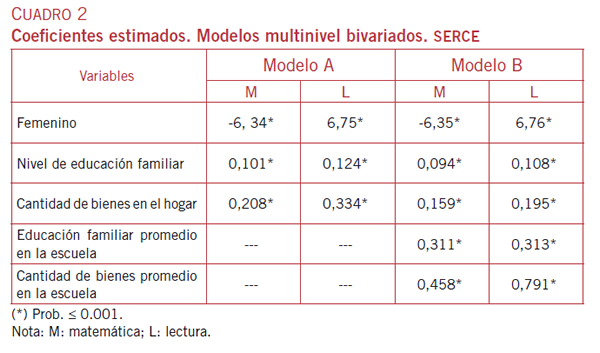
Para avalar estadísticamente las precedentes interpretaciones basadas en el cuadro 1, las variables bien y edu son incorporadas en la parte fija del modelo anterior y se reprocesa el modelo (cuadro 2, modelo A).

Las estimaciones de las distancias de rendimiento promedio de hombres y mujeres (matemática = -6,34; lectura = 6,75) no han variado significativamente respecto de las estimaciones presentadas con anterioridad. Por tanto, el género tiene efecto aditivo propio, es decir, persiste la inequidad aun cuando se «controle» el origen social del alumno.

En el modelo B se han incorporado los indicadores del contexto socioeconómico de la escuela. Ambos coeficientes son altamente significativos en ambas disciplinas. De hecho, este modelo explica 30,5% y 25,8% de las variaciones inter-países en matemática y lectura.

Finalmente, los coeficientes que indican las diferencias de género no se modifican y, por tanto, el efecto del género se mantiene más allá de la incidencia del contexto socioeconómico escolar.

Ahora se pretende responder al interrogante acerca de si el efecto de los factores extraescolares considerados difiere según el sexo del alumno. Para ello, se crean dos términos interactivos de género y se los introduce en la parte fija del modelo sin aleatorización, junto con los dos indicadores de nivel socioeconómico de la familia del alumno (cuadro 3, modelo A).

Con excepción de la interacción entre género y bienes en matemática, los tres términos interactivos restantes son significativos. Dado la definición de ambas variables implicadas y el signo positivo de los tres términos, se infiere que la incidencia de los factores extraescolares individuales del alumno es más intensa entre las mujeres que entre los hombres. Esta inferencia es más robusta respecto de lectura, donde ambos indicadores exógenos resultan altamente significativos.

Entonces, la ventaja de las mujeres respecto de los hombres en el aprendizaje de la lectura disminuye a medida que disminuye el nivel económico familiar. Los niveles de logro de hombres y mujeres en lectura son más similares entre las familias de menores ingresos, mientras que entre aquellas que son económicamente más aventajadas, tal diferencia se acentúa de forma llamativa. En matemática la relación se invierte: a medida que disminuye el nivel educativo familiar, se amplía la distancia entre géneros, a favor de los varones (p £ 0,0098).

La incorporación de los dos indicadores de contexto socioeconómico escolar (modelo B) no altera los coeficientes de interacción; por tanto, la conclusión anterior es válida cualquiera sea la composición socioeconómica de la escuela.

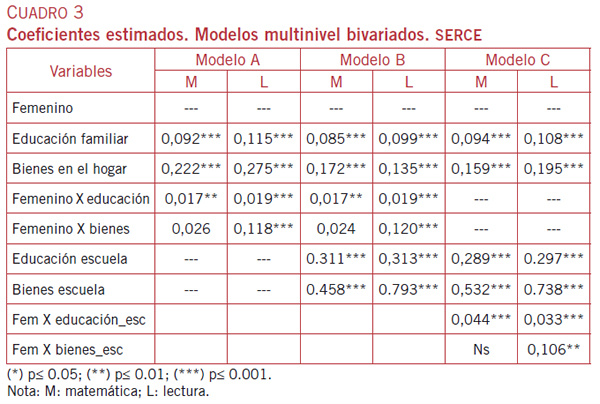
El gráfico 1 muestra las distancias relativas entre los promedios de ambos géneros en cada uno de los quintiles de educación familiar (edu) y bienes y servicios (bien) en el hogar. En general, las tendencias de ambas disciplinas son inversas. A medida que se asciende en el nivel socioeconómico, las distancias en matemática disminuyen, mientras que las de lectura aumentan. Entre las poblaciones más carenciadas, la ventaja de las niñas en lectura se acortan, mientras que la de los varones en matemática se amplía.

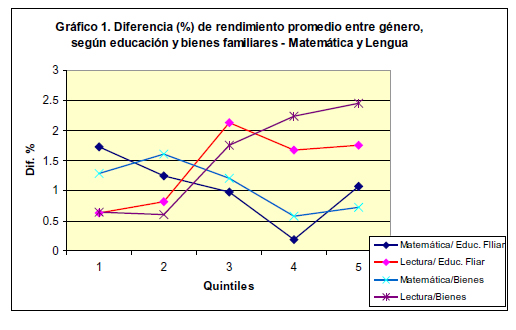
Finalmente, en el modelo C la interacción está definida respecto de la composición socioeconómica de la escuela. Todos los coeficientes, con excepción de la interacción entre género y bienes promedio en la escuela respecto de matemática, son significativos; por tanto, la intensidad del efecto género varía según el nivel socioeconómico: cuando el nivel socioeconómico del alumnado disminuye, la ventaja de la mujer en lectura tiende a desaparecer.

Hasta aquí se ha supuesto que la distancia hombre-mujer es fija a lo largo de todos los países. Ahora se libera este supuesto especificando el género como un coeficiente aleatorio en el nivel paísdel modelo sin ningún «control» socioeconómico. Los resultados son:

Los términos aleatorios son el intercepto de matemática (ƒ0) y de lectura (ƒ1), seguido por la diferencia masculino-femenino en matemática (ƒ2) y en lectura (ƒ3).

En los cálculos, las covarianzas entre el puntaje promedio en una disciplina y las distancias hombre-mujer en la otra disciplina (s2ƒ12 y s2ƒ03) se asumen igual a 0 (cero), dado su poco interés interpretativo. Además, los procesamientos demostraron que los coeficientes de covariación entre las distancias entre géneros y los rendimientos promedios del país en matemática (s2ƒ02) y en lectura (s2ƒ13) no son significativos, es decir, el rendimiento promedio no permite predecir la inequidad de género.

En este modelo todas las estimaciones resultan significativas, lo cual permite concluir que:

Estas estimaciones indican gran disparidad entre los países de la región. En algunos, la distancia hombre-mujer a favor del hombre en matemática es muy amplia, mientras que en otros no es estadísticamente significativa o, inclusive, la relación se invierte. Si se atiende a los coeficientes estimados para cada país y cada disciplina, en cinco de ellos no existe diferencia de género en matemática pero sí en lectura, con ventaja para las mujeres; en otros cinco, esta relación se invierte: los hombres superan a las mujeres en matemática pero no existen diferencias en lectura; en dos países los hombres superan a las mujeres en ambas disciplinas, mientras que en uno (Cuba) se verifica la situación inversa; finalmente, en un solo país (Brasil) la mujeres rinden menos en matemática pero más en lectura. En la mayoría de los países los hombres aventajan a las mujeres en matemática y no hay diferencias en lectura, o las mujeres aventajan en lectura y no hay diferencia en matemática. Se constata también que, entre los países, las varianzas de los puntajes de los hombres, tanto en matemática (2532,8) como en lectura (1925,8) son menores que las de las mujeres. Los países son más homogéneos respecto de los resultados obtenidos por los hombres, comparado con los resultados de las mujeres.

Finalmente, este modelo fue reprocesado incorporando las variables de «control» socioeconómico: ninguno de los coeficientes aleatorios se alteró; por tanto, las variaciones inter-país e intra-país (entre escuelas) no están relacionadas con las condiciones socioeconómicas, ni del alumno ni de la escuela.

En el 6.° grado de la educación primaria de América Latina, los alumnos obtienen mejores resultados en matemática que las alumnas, y a su vez, las niñas se desempeñan mejor que los niños en lectura. El tamaño de estas brechas de género varía de país a país. Al igual que en otras regiones de países en desarrollo, esta variación parece ser más intensa que en los países desarrollados. Con base en el criterio de significación estadística adoptado, en la mayoría de los países solo acontece uno de los términos de este patrón de desigualdad. Esto podría indicar que en algunos países existen prácticas más eficaces para reducir la brecha de género en una o ambas asignaturas.

Pero más allá de la significación estadística de las diferencias de género en cada país, el análisis constató que a medida que la intensidad de la desigualdad de género aumenta en matemática, también aumenta la desigualdad en lectura, y viceversa, es decir, la correlación entre las dos desigualdades es muy alta.

Como ha sido confirmado por estudios previos, el nivel y la distribución de los logros en ambas materias escolares se ven fuertemente afectados por el origen social del alumno y por la composición socioeconómica de la escuela. El principal aporte de este estudio es haber demostrado la importancia de relacionar esos factores exógenos con las desigualdades de género.

Con este enfoque, se ha podido constatar que la ventaja de los varones en matemática se mantiene en todos los quintiles de nivel socioeconómico familiar, comportamiento que también se verifica con el predominio de las mujeres en lectura. El género afecta los logros escolares incluso cuando el nivel socioeconómico ha sido «controlado» estadísticamente. Pero, al mismo tiempo, se encontró que la superioridad de las niñas en lectura depende del nivel socioeconómico. El promedio de lectura de los varones en un nivel socioeconómico dado siempre es superior al promedio de las mujeres en el nivel socioeconómico inmediato inferior. La superioridad de los varones en matemática exhibe el mismo comportamiento.

Esta perspectiva permitió constatar también que las niñas son más afectadas por la condición socioeconómica familiar que los varones. Ello es más evidente en lectura, donde entre las familias de bajos ingresos, mujeres y varones tienden a obtener logros similares, mientras que en matemática la relación se invierte: a medida que el nivel educativo familiar disminuye, la brecha de género se ensancha en favor de los varones. En el extremo más bajo de la escala socioeconómica, niños y niñas están con el mismo riesgo de fracaso en lectura, mientras que en matemática, el riesgo de fracaso es mucho mayor para las niñas.

Además, el análisis mostró que el efecto género en lectura varía según el contexto socioeconómico de la escuela: en las escuelas con un alumnado más desfavorecido socialmente, la ventaja de las mujeres en lectura tiende a desaparecer, es decir, en las escuelas con población más pobre, niñas y niños tienen el mismo riesgo de fracaso.

Todos estos hallazgos demuestran que las cuestiones de género en el aprendizaje escolar deberían ser incluidas en la agenda política de los países de América Latina. En varios países fuera de la región se ha producido una extensa bibliografía conteniendo diversas hipótesis teóricas para explicar las diferencias de género en los logros educativos. De acuerdo a los resultados presentados aquí, parece justificado promover estudios dirigidos a profundizar en el conocimiento sobre las causas subyacentes de las desigualdades de género en los logros educativos también en los países de la región.

BIBLIOGRAFÍA

Arnot, M., David, M. y Weiner, G. (1996). Educational reforms and gender equality in schools. Manchester: Equal Opportunities Commission.

Bishop, J. H. (1992). «The impact of academic competencies on wages, unemployment, and job performance». Carnegie-Rochester Conference Series on Public Policy,37, pp. 127-194.

Blanco, B. (2008). «Factores escolares asociados a los aprendizajes en la educación primaria mexicana: un análisis multinivel». Revista Iberoamericana sobre Calidad, Eficacia y Cambio en Educación,6(1), pp. 58-84.

Boissiere, M., Knight, J. y Sabot, R. (1985). «Earnings, schooling, ability, and cognitive skills». American Economic Review, 73(5), pp. 1016-1030.

Buckingham, J. (1999). «The puzzle of boys’ educational decline». Issue Analysis, 9, pp. 1-11.

Cervini, R. (2010). «Análisis comparativo de los condicionantes extraescolares del desempeño de los alumnos de 3.º y 6.º año en Matemática y en Lengua de la educación primaria (one/2007) - Modelos multinivel bivariados». Documentos Pedagógicos. Dirección Nacional de Información y Evaluación de la Calidad (diniece).

Cervini, R. (2012), «El ‘efecto escuela’ en países de América Latina: Reanalizando los datos del serce». Archivos Analíticos de Políticas Educativas, 20(39). Disponible en: http://epaa.asu.edu/ojs/article/view/1086.

Currie, J. y Duncan, T. (2001). «Early test scores, school quality and ses: longrun effects on wage and employment outcomes». Research in Labor Economics, 20, pp. 103-132.

doee (1998). Informe de resultados. Tercer curso. Asunción: Dirección de Orientación y Evaluación Educativa.

Entwisle, D., Alexander, K. y Olson, L. (1994). «The gender gap in Math: Its possible origins in neighborhood effects». American Sociological Review, 59, pp. 822-838.

Entwisle, D., Alexander, K. y Olson, L (2007). «Early schooling: The handicap of being poor and male». Sociology of Education, 80(2), pp. 114–138.

FernándezAguerre, T. (2002). «Determinantes sociales e institucionales de la desigualdad educativa en sexto año de educación primaria de Argentina y Uruguay, 1999. Una aproximación mediante un modelo de regresión logística». Revista Mexicana de Investigación Educativa, 7(16), pp. 501-536.

Franco, C. y otros (2007). «Qualidade e eqüidade em educaçao: reconsiderando o significado de ‘factores intra-escolares’». Ensaio: Avaliaçao e Políticas Públicas em Educaçao, 15(55), pp. 1-15.

Hedges, L. y Nowell, A. (1995). «Sex differences in mental test scores, variability, and numbers of high-scoring individuals». Science, 269, pp. 41-45.

Hinshaw S.P. (1992). «Externalizing behavior problems and academic underachievement in childhood and adolescence: causal relationships and underlying mechanisms». Psychol. Bull. 111(1), pp. 127–155.

Hyde, J. y Linn, M. (eds) (1986). The psychology of gender: advances through metaanalysis.Baltimore, MD: John Hopkins University.

iimec (1997). Informe nacional sobre el desarrollo, validación y aplicación de las pruebas de diagnóstico de conocimientos. San José de Costa Rica: Ministerio de Educación Pública.

Leahey, E. y Guo, G. (2001). «Gender differences in mathematical trajectories». Social Forces, 80, pp. 713-732.

llece (2001). Primer estudio internacional comparativo sobre lenguaje, matemática y factores asociados, para alumnos del tercer y cuarto grado de la educación básica. Informe técnico. Santiago: Laboratorio Latinoamericano de Evaluación de la Calidad de la Educación, orealc/unesco.

llece (2008). Reporte técnico serce. Oficina Regional de Educación para América Latina y el Caribe de la unesco. Santiago: Laboratorio Latinoamericano de Evaluación de la Calidad de la Educación, orealc/unesco.

Marks, G. (2008). «Gender difference in the effects of socioeconomic background: Recent cross-national evidence». International Sociology, 23(6), pp 845-863.

Ministerio de Educación de Perú (2001). «Resultados de las pruebas de matemática y lenguaje: ¿Qué aprendimos a partir de la evaluación crecer 1998?» Unidad de Medición de Calidad Educativa (umc), Boletín umcn.° 5/6, Lima: Ministerio de Educación. Disponible en: www2.minedu.gob.pe/umc/admin/images/publicaciones/boletines/Boletin-0506.pdf.

Mullis, I., Martin, M. y Foy, P. (2005). iea’s timss 2003 International report on achievement in the mathematics cognitive domains - Findings from a developmental project. Chestnut Hill: timms y pirls International Study Centre.

Mullis, I. y otros (2007). pirls 2006 International report. iea’s progress in international reading literacy achievement in primary school in 40 countries. Chestnut Hill: timms y pirls International Study Centre.

Murnane, R., Willett, J. y Levy, F. (1995). «The growing importance of cognitive skills in wage determination». Review of Economics and Statistics, 77(2), pp. 251- 266.

Rivera-Batiz, F. (1992). «Quantitative literacy and the likelihood of employment among young adults in the United States». Journal of Human Resources, 27(2), pp. 313-328.

simecal (1998). Rendimientos de 3.° y 6.° de educación primaria en lenguaje y matemática y factores asociados.La Paz: Ministerio de Desarrollo Humano.

Tsui, M. (2007). «Gender and Mathematics achievement in China and the United States». Gender Issues, 24, pp. 1-11.

Universidad Pedagógica Nacional (1998). Factores asociados al rendimiento académico.Honduras: Secretaría de Educación.

Wilder, G. y Powell, K. (1989). «Sex differences in rest performance: a survey of the literature». Educational Testing Service Research Report, n.° 4. Princeton, NJ: Educational Testing Service.

Willingham, W. y Cole, N. (1997). «Research on gender differences». En W. Willingham y N. Cole (eds.), Gender and fair assessment.Hillsdale, NJ: Lawrence Erlbaum.

Won, K., Lam, W. y Ho, L. (2002). «The effects of schooling on gender differences». British Educational Research Journal, 28(6), pp. 827-843.

Resultados no expuestos aquí indicaron que también los coeficientes relativos a la aleatoriedad del nivel escuela son significativos y, por tanto, las constataciones referidas al nivel país son extrapolables a las variaciones inter-escuela dentro de los países.

Número 68 Mayo-Agosto / Maio-Agosto 2015

Género y rendimiento escolar en América Latina. Los datos del SERCE en matemática y lectura